基礎知識：

      BCD：BCD碼又稱為8421碼，

      意義：之所以有時候需要將binary轉換為BCD，一般是用在本科的實驗中，為了將binary顯示在數碼管中，當然還有很多應用，只是目前我還沒有用到。

轉換算法：左移加3法

      移位加3法的具體原理，在網上感覺也沒有人能夠說的清楚，以后找到書籍再說吧。下面解釋下左移加三算法。這里以8bit二進制數FF做例子。

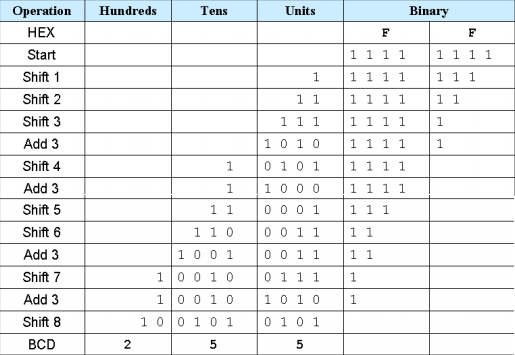
該算法的操作為上圖。下面對上圖的操作進行詳細的解釋：

      由于8bit的二進制最大為FF，轉換為十進制為255。所以需要使用三個BCD碼來表示所有的8bit二進制數。上圖的hundreds表示百位的BCD，tens表示十位的BCD，Units表示個位的BCD。算法的操作為一直將binary數據左移，移出的數據按順序存在hundreds，tens，Units。例如上面的shift1，shift2，shift3操作后，Units變為了0111，至于為何在shift3后進行add3操作，是因為在算法中每一次左移，都要對hundreds，tens和Units進行判斷，如果hundreds，tens和Units里面的值大于或等于5，就將hundreds，tens和Units自加3.所以shift3后，Units里面為0111，表示為7，此時不能左移，而是對Units加三操作，所以Units的值從0111變為了1010.值得注意的是，只要hundreds，tens和Units中任意一個的值大于或等于5（0101），就要先進行一次自加三的操作，然后才能繼續左移，后面的操作同上。

注意2：n位的binary就需要進行n次左移

注意3：最后一次左移不需要進行add3操作

注意4 :  親自推導16位的，和24位的binary轉換，結果正確，所以該算法適用于任意位binary

to  BCD，當然這種論斷沒有足夠的理論依據。

verilog代碼：

說明：對于8bit及以下的binary，可以使用case語句實現移位加三算法。由于這里說明的是任意位的二進制數，轉為BCD，所以我的代碼中設計了一個狀態機，來控制移位，加三和結束操作。由于代碼編寫時間倉促，其中或許有些bug。

//name: 二進制轉BCD
//data: 2014-04-17 at kb129
//info: as 2**8=255  change to BCD then this need 3 times of “8421”
module b_to_bcd(
      clk,
      rst_n,
      binary,
      state_en,
     BCD
);
parameter   b_length      = 8;
parameter   bcd_len       = 12;
parameter   idle              = 5'b00001;
parameter   shift             = 5'b00010;
parameter   wait_judge   = 5'b00100;
parameter   judge           = 5'b01000;
parameter   add_3          = 5'b10000;

input       clk;
input       rst_n;
input    [b_length-1:0]  binary;
input      state_en;
output reg [bcd_len-1:0]  BCD;

reg  [b_length-1:0]  reg_binary;     
reg  [3:0]    bcd_b, bcd_t, bcd_h;
reg  [3:0]    shift_time;                    
reg   [5:0]    c_state, n_state;
reg      add3_en;
reg      change_done;
//this is a three section kind of state code style
always@(posedge clk or negedge rst_n)

begin
        if(!rst_n)
              c_state <= idle;
       else
             c_state <= n_state;
end
//the second section
always@(posedge clk or negedge rst_n)
begin
       if(!rst_n)
                  c_state <= idle;
       else
                 case(n_state)
                 idle:begin
                               if((binary!=0)&&(state_en==1'b1)&&(change_done==0'b0))
                                       n_state <= shift;
                              else
                                      n_state <= idle;
                          end
                 shift: n_state <= wait_judge;
       wait_judge: begin
                               if(change_done==1'b1)
                                      n_state <= idle;
                               else
                                      n_state <= judge;
                          end
                judge:begin   
                                if(add3_en)
                                       n_state <= add_3;
                               else
                                       n_state <= shift;
                          end
                add_3:begin
                                 n_state <= shift;
                           end
               default: n_state <= idle;  
              endcase
end
//the third section
always@(posedge clk or negedge rst_n)
begin
         if(!rst_n)
                  begin
                          shift_time  <= 4'b0;
                          change_done <= 1'b0;
                          add3_en  <= 1'b0;
                 end
         else
           case(n_state)
           idle:begin
                          shift_time <= b_length;
                          reg_binary <= binary;
                          bcd_h     <= 4'b0;
                          bcd_t     <= 4'b0;
                          bcd_b     <= 4'b0;      
                  end
          shift:begin 
                      {bcd_h,bcd_t,bcd_b,reg_binary} <= {bcd_h,bcd_t,bcd_b,reg_binary}<<1;
                      shift_time <= shift_time-1;
                      if(shift_time==1)     change_done <= 1'b1;
                      else                       change_done <= 1'b0;    
                 end
  wait_judge:begin
                       if((bcd_h>=4'd5)||(bcd_t>=4'd5)||(bcd_b>=4'd5))
                               add3_en <= 1;
                       else
                               add3_en <= 0;
                      if(change_done==1)   BCD <= {bcd_h,bcd_t,bcd_b};
                    end
        judge:  add3_en <= 0;
       add_3: begin
                       if(bcd_h>=4'd5) bcd_h <= bcd_h + 4'b0011; else bcd_h <= bcd_h;
                       if(bcd_t>=4'd5) bcd_t <= bcd_t + 4'b0011; else bcd_t <= bcd_t;
                       if(bcd_b>=4'd5) bcd_b <= bcd_b + 4'b0011; else bcd_b <= bcd_b;
                   end
      default: begin
                           change_done <= 1'b0;
                           add3_en  <= 1'b0;
                  end
           endcase
        end
endmodule

代碼的仿真：這里對上面的代碼進行了仿真，仿真結果顯示上面代碼可以實現8bitbinary的BCD轉換。

testbench：

module  filter_tb;
reg clk;
reg rst_n;
reg state_en;
reg  [7:0] binary;
wire [11:0] BCD;
initial
       begin
                clk=0;
                rst_n=0; 
                state_en = 0;
     #100   binary = 8'h3f;
     #150   rst_n=1;
     #200     state_en =1;
end
always  #10  clk=~clk;
b_to_bcd u_b_to_bcd
(
 .clk(clk),
 .rst_n(rst_n),
 .binary(binary),
 .state_en(state_en),
 .BCD(BCD)
);
endmodule
仿真結果：二進制的3f=十進制的63

相關文章