已知 :
unsigned int temp=1000;
要求出result = value * 10%
最直接的方法是
使用位運算的方法是 :
在MPLAB(PICC-V9.70-Lite Mode)下測試得到的結果顯示使用位運算需要的時間僅為乘除法運算的4分之1。
先看測試代碼、比較一下兩種表示方法,再來看如何使用位運算的表示方法。
測試代碼 :
#include
__CONFIG(0x3f3a);
unsigned int temp=1000;
unsigned int result1=1;
unsigned int result2=1;
int main(void)
{
}
在MPLAB中沒有更改晶振、的按默認的20MHz調試的。
使用’ asm("nop");’是為了調試的方便。
結果為 :result1 = 97、result2 = 100;
由位運算求出的10%誤差是3%、而乘除法的結果沒有誤差。
在很多情況下都不需要絕對精確的結果、所以上面的差值3是完全可以接受的。
下面來看看使用位運算和乘除法需要的執行時間 :
|
|
Instruction Cycles
|
Time(uSecs)
|
|
位運算
|
222
|
444
|
|
乘除法
|
851
|
1702
|
使用位運算需要的時間大概是乘除法運算的4分之1。
在反匯編代碼中可以看到、乘除法運算過程中調用了乘法和除法的函數(是MPLAB自帶的) :
乘法 :
即0x709處定義的乘法 :
除法 :
即0x734處定義的除法:
執行乘發和除法需要的時間為 :
|
|
Instruction Cycles
|
Time(uSecs)
|
|
__wmul
|
305
|
610
|
|
__lwdiv
|
505
|
1010
|
執行乘法或除法需要的時間都遠遠比整個位運算多得多。
使用這種位運算有幾個限制條件 :
1、需要知道系數、比如上面的10%、當然、這個系數是120%、或是8倍都是一樣的。
2、結果允許一定的誤差、比如上面的97、差值是3。這個誤差可大可小、接下來會講到。
現在來看看上面使用的位運算 :
求temp的10%的表達式
result = (temp >> 4) + (temp >> 5) + (temp >> 8) + (temp >> 9);
是怎么來的呢。
x/64、用移位表示就是x>>6、知道這種表示法、自然就會明白了。
10%用二進制表示出來就是 :
1/(2^4) + 1/(2^5) + 1/(2^8) + 1/(2^9) = 0.099609375、即9.96%、約等于10%。
所以結果就是 :
= temp * (
= temp / (2^4) + temp / (2^5) + temp / (2^8) + temp / (2^9)
= (temp >> 4) + (temp >> 5) + (temp >> 8) + (temp >> 9)
這里注意要加括號’()’、因為移位運算的優先級比加減法低
10%用到減法來表示的情況 :
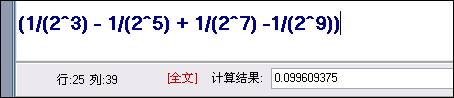
(1/(2^3) - 1/(2^5) + 1/(2^7) -1/(2^9)) = 0.099609375
計算時使用天下計算器之類的計算軟件會很快的得到結果 :
誤差 :
方法很簡單、但是要注意誤差的存在。
我們的表達式里面有4個部分1/(2^4) + 1/(2^5) + 1/(2^8) + 1/(2^9)、
如果只要三項1/(2^4) + 1/(2^5) + 1/(2^8)、結果就是0.09765625=9.76%
誤差增大了、要得到越小的誤差、需要的項數就越多。
使用5項時誤差更小1/(2^4) + 1/(2^5) + 1/(2^8) + 1/(2^9) + 1/(2^11)= 0.10009765625=10.00%。
但是使用的項數運算量越大,而且移位的位數越大、運算量也越大。
temp>>9需要移位次、temp>>11需要移位10次。
所以只要誤差可接受即可、不必耗費更多的代價來得到更高的精度。
空間 :
當然、最好的方法還是將結果做成數組、使用查表取值。
沒有運算、不用考慮耗時、也不用擔心運算出錯。
比如將255分成100份 :
const unsigned char table[100]={
2, 5, 7, 10, 12, 15, 17, 20, 22, 25,
……
.
……
};
耗費flash中的100個Byte并不算多、很多時候flash都用不完的。
'1/(2^1)=0.5
'1/(2^2)=0.25
'1/(2^3)=0.125
'1/(2^4)=0.0625
'1/(2^5)=0.03125
'1/(2^6)=0.015625
'1/(2^7)=0.0078125
'1/(2^8)=0.00390625
'1/(2^9)=0.001953125
'1/(2^10)=0.0009765625