1卷積演示程序設計原理

數字信號處理的直接對象是數字信號，處理的方式是數值運算的方式，它涉及到的內容非常豐富和廣泛，它是應用最快、成效最顯著的新學科之一，作為信息專業的專業基礎課，需要掌握其基本理論和基本的分析方法，通過理論實踐、原理和應用結合掌握知識。而MATLAB是集數學計算、圖形處理和程序語言設計于一體的軟件，通過MATLAB來實現數字信號處理的有關表達，最終實現課程設計的目的。

• 卷積演示程序設計要求
  

（1）序列的長度和內容由運行時輸入；

（2）分別動態演示它們進行線性卷積和循環卷積的過程，要求體現翻轉、移位、相乘、求和等過程；

（3）根據卷積結果，分析兩類卷積的關系。

• 卷積演示程序設計目的
  

(1)、通過基于MATLAB的算法仿真實驗及分析，進一步領會和深化課堂上學到的有關數字信號處理的基本概念、基本原理以及基本的信號處理操作及設計方法。

(2)、掌握線性卷積與圓周卷積軟件實現的方法，并驗證二者之間的關系。

1.2 卷積演示程序設計內容

（1）可輸入任意2待卷積序列x1(n)、x2(n)，長度不做限定。測試數據為：

x1(n)={1,1,1,1,0, 0,1,1,1,1,0,0}，x2(n)={0,1,2,1,0,0,0,1,2,1,0,0}；

（2）分別動態演示2序列進行線性卷積x1(n)﹡x2(n)和圓周卷積x1(n) x2 (n)的過程；要求分別動態演示翻轉、移位、乘積、求和的過程。

（3）圓周卷積默認使用2序列中的最大長度，但卷積前可以指定卷積長度N用以進行混疊分析。

（4）根據實驗結果分析2類卷積的關系。

2卷積演示程序總體設計及關鍵技術分析

2.1 卷積演示程序設計基本原理

2.1.1 線性卷積

線性時不變系統（Linear Time-Invariant System, or L. T. I系統）的輸入、輸出間的關系為：當系統輸入序列為x(n)，系統的單位脈沖響應為h(n)，輸出序列為y(n)，則系統輸出為：

或   

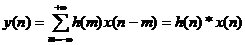
上式稱為離散卷積或線性卷積。

2.1.2 圓周卷積

設兩個有限長序列x1(n)和x2(n)，均為N點長

x1(n) 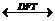 X1(K)

x2(n) 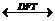  X2(K)

如果X3(K)=X1(K)﹒X2(K)

則

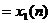N

上式稱為循環卷積或圓周卷積

注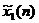：為x1(n)序列的周期化序列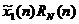；為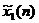的主值序列。

編程計算時，x3(n)可表示如下：

2.2 兩個有限長序列的線性卷積

序列x1(n)為L點長，序列x2(n)為P點長，x3(n)為這兩個序列的線性卷積，則x3(n)為

且線性卷積x3(n)的最大長L+P-1，也就是說當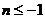和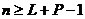時x3(n)=0。

2.3 兩個有限長序列的圓周卷積

線性卷積是求離散系統響應的主要方法之一，許多重要應用都建立在這理論基礎上，如卷積濾波等，專用函數conv（x,h）可完成線性卷積過程。

圓周卷積的計算速度遠快于線性卷積，如果選擇圓周卷積的長度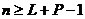,則可以用圓周卷積取代線性卷積。方法如下：

• 定義圓周卷積的長度：選擇N=L+P-1。
• 將兩個序列的長度都補足為N:
  

將長為L的序列x1(n)延長到N，補N-L個零；

將長為P的序列x2(n)延長到N，補N-P個零；

• 翻轉x1(n)，周期延拓為序列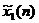，取主周期。
• 循環移位：與線性卷積不同，圓周卷積運算中采用的是循環移位，有限長序列x1(n)的循環移位定義為：
  

其含義如下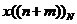：表示x(n)的周期延拓序列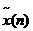的移位：

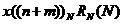            表示對移位的周期序列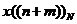取主值序列。所以f(n)仍然是一個長度為N的有限長序列。

2.4 卷積演示程序設計思想

首先建立一個基本的框架，制作一個菜單，其中包括主程序菜單和子程序的菜單，子程序菜單可以選擇回到主程序菜單選擇功能。菜單的框架完成后，實現可以任意輸入兩個序列，然后分別制作動態演示序列的線性卷積的程序、動態演示序列的圓周卷積、以及驗證時域卷機定理以及比較運行速率的程序。結合上面建立的框架完成菜單選擇以及功能的調用，讓整個設計完美。

2.4.1卷積演示程序設計流程圖

卷積演示程序設計流程圖如圖1所示：

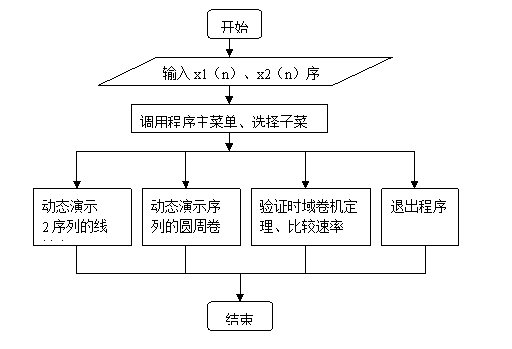
圖1  流程圖

2.4.2卷積演示程序關鍵技術分析

本個設計主要要實現動態的演示，為實現動態演示，有很多不同的方法，而我采用的是for循環加上pause，在for循環中的一次執行中，實現一次繪圖，表示某一時刻的狀態，用pause暫停等待for循環中下一次執行，實現動態演示。這是主要的一個設計，另外一個重要的技巧是如何將循環卷積表示出來，因為循環卷積的結果是周期的，其循環卷積的方法和線性卷積不同，并且循環卷積中要處理幾種情況：如當x1序列和x2序列之間的最大長度比卷積N長度大時是一種畫圖方法，比它小時是另外一種方法，然而困難的是當循環卷積長度比序列最大長度小時還要分析x1和x2序列各自長度與N的關系而做不同的情況分析，具體的解決方法見程序實現。

3卷積演示程序

3.1程序實現

3.1.1線性卷積程序實現

x1=[1,1,1,1,0,0,1,1,1,1,0,0];

x2=[0,1,2,1,0,0,0,1,2,1,0,0];

p=length(x1);

q=length(x2);

n=p+q-1;

a= 0 : q-1;

y2(a+1)=x2(q-a);

for n=1 : p+q-1

k=-q+n:1:-1+n;

subplot(3,1,2)

stem(k,y2)

title('x2(n-m)');

axis([-16,16,0,24]);

以上部分是實現翻轉并移位，在設計中是將序列x2進行翻轉和移位。

y=conv(x1,x2);

t=1:1:n

h(t)=y(t);

subplot(3,1,3)

t=0:n-1;

stem(t,h);

title('線性卷積y(n)')

axis([-16,16,0,24]);

pause(1)

end

以上整個部分就是實現線性卷積的過程。

subplot(3,2,1)

stem(x1);

title('x1(m)')

axis([0,15,0,1]);

pause(1)

subplot(3,2,2)

stem(x2);

title('x2(m)')

axis([0,15,0,2]);

pause(1)

end

3.1.2圓周卷積程序實現

對于循環卷積，要求我們進行判斷并根據情況做不同的分析：

x1=[1,1,1,1,0,0,1,1,1,1,0,0];

x2=[0,1,2,1,0,0,0,1,2,1,0,0];

p=length(x1);q=length(x2);k=max(p,q);%p<q

if k>N

    if p<q&p<N

x11=[x1,zeros(1,N-p)];

n=0:1:N-1;

x22(n+1)=x2(n+1);

elseif p==q|p>N

    n=0:1:N-1;

x11(n+1)=x1(n+1);

x22(n+1)=x2(n+1);

else disp('錯誤，x1的長度要比x2短')

end

3.2結果及分析

開始運行程序，會進入主菜單，按照提示進行選擇：

請輸入x1:[1,1,1,1,0,0,1,1,1,1,0,0]

請輸入x2:[0,1,2,1,0,0,0,1,2,1,0,0]

（1）、動態演示2序列的線性卷積

圖2   線性卷積結果

（2）、動態演示2序列的10點的圓周卷積

圖3  圓周卷積結果

4結論

針對卷積演示的程序進行設計，并給出了兩個示例序進行線性卷積和圓周卷積的翻轉、移位、乘機、求和的過程等。圓周卷積是將所有數據限定一個固定的長度。設線性卷積和圓周卷積有用信號部分長度分別為L、P，則當圓周卷積長度大于等于L+P-1時兩者等價。

線性卷積和圓周卷積對運算有不同的要求：線性卷積的對象可以是有限長或無限長非周期序列，若兩個序列的長度分別為M和N，則卷積后的序列長度為L=M+N-1。圓周卷積的對象是兩個同長度（若長度不同可用補零的方法達到同長度）的有限長序列，圓周卷積的結果也是同一長度的有限長序列。

它們的關系是：圓周卷積是線性卷積L點周期延拓的主值區間。

5心得體會

通過本次論文設計鞏固了所學過的數字信號處理課程的有關知識，同時也對matlab這個軟件有了更深的了解，它與數字信號處理這門課程之間有著緊密關系，matlab中是采用數組和距陣的方式處理數據，如何將數字信號處理有關的資料以數組和距陣進行編程是我們學習的一個方面，通過這次的課程設計，讓我發現了數字信號處理在matlab中的應用，同時也激發了我利用這軟件來實現數字信號處理有關問題的興趣。

本次設計中，有機地結合了理論與實踐，既考察了我們對理論知識的掌握情況，還反映出我們實際動手能力和編程能力，更主要的是它激起我們創新思維，提高了自己獨立分析問題和解決問題的能力，這在無形中以及提高了我各方面的能力。無論是在知識上，還是在思想上都給我烙下了深刻的印象。

完整的Word格式文檔51黑下載地址：

基于 MATLAB 的卷積演示系統.doc (69 KB, 下載次數: 29)