里面有源文件和仿真結果,與分析
信號頻率估計 信號頻率估計是信息科學在信號處理領域的一個重要的組成部分,指的是通過對信號采樣值的計算和變換,估計出淹沒于噪聲中的信號頻率。按照信號的平穩性差異,可將頻率估計方法分為平穩信號頻率估計與非平穩信號頻率估計。 平穩信號頻率估計始于1822年,傅里葉提出諧波分析理論,奠定了信號分析和功率譜估計理論基礎。在19實際末,Schuster提出周期圖概念,至今沿用。在1958年,Blackman和Tukey提出自相關譜估計,簡稱BT法。以上幾種方法為信號頻率估計經典法。經典法的缺點是分辨力低(為1/N,N為數據長度),提高分辨力需增加數據長度N,從而增加運算時間。對此,提出了修正平均周期圖法(Welch法)、Bartlett法等。 在60年代末70年代初,科學家們提出使用現代法來進行信號的頻率估計,以提高頻率分辨率。現代法分為兩類:參數估計法,非參模型法。參數估計法包括:自回歸(AR)模型,滑動平均(MA)模型,自回歸滑動平均(ARMA)模型。參數估計法具有較好的頻率分辨能力,運算速度較快,但性能受參數的選取等因素的影響。非參數模型法包括:最大似然法,最小方差無失真法(MVDR),多信號分類法(MUSIC),子空間旋轉不定法(ESPRIT)。 對于非平穩信號來說,瞬時頻率隨時間變化,時頻分布能夠更準確的分析信號的時變本質,讓分析精確到具體時間和特定的頻率上,使用的方法有Gabor變換,短時傅里葉變換,小波變換,S變換,Hilbert-Huang變換等。 下面具體介紹不同的信號頻率估計方法。 1、周期圖法(Periodogram) 周期圖法通過計算采樣信號的FFT,獲得離散點的幅度,然后取其幅頻特性的平方并除以序列長度N。 由于序列x(n)的離散傅里葉變換X(ejw)具有周期性,因而這種功率譜也具有周期性,被稱為周期圖。因其直接觀察數據的傅氏變換,又被稱為直接法。周期圖是信號功率譜的一個有偏估值,隨著所取信號序列的長度的不同,所得到的周期圖也不同。應用時,要在方差、偏差、分辨率之間進行折中選擇。 2、自相關函數法(BT法) 設uN(n)為u(n)的N個觀測值,則u(n)的自相關函數估計值為 根據維納-辛欽(Wiener-Khintchine)定理,對上式求傅里葉變換 因為上式是通過自相關函數間接得到的,又稱為間接法。因為 當m和N都比較大時,計算量很大。 接下來介紹現代法中的參數估計法。 參數估計法的基本思路:1、參數模型假設研究過程是由一個輸入序列u(N)激勵一個線性系統H(z)的輸出。2、由假設參數模型的輸出x(n)或其自相關函數來估計H(z)的參數。3、由H(z)的參數估計x(n)的功率譜。所以參數模型功率譜的求解有兩步:1、H(z)模型參數估計2、依據模型參數求功率譜。 3、AR模型法 x(n)的功率譜可表示為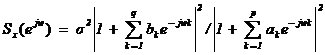 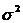 是激勵白噪聲的方差,Sx(ejw)為功率譜密度,ak和bk為模型參數。若式中參數b1,b2,…,bq全為0,則上式變為 是激勵白噪聲的方差,Sx(ejw)為功率譜密度,ak和bk為模型參數。若式中參數b1,b2,…,bq全為0,則上式變為 即為AR模型。 即為AR模型。AR模型又稱為自回歸模型,是一個全極點模型。該模型現在的輸出是現在的輸入和過去p個輸出的加權和: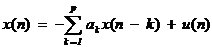 ,式中u(n)為白噪聲信號,p為AR模型的階數。對上式求z變換,得到系統函數: ,式中u(n)為白噪聲信號,p為AR模型的階數。對上式求z變換,得到系統函數: 由隨機信號通過線性系統理論知輸出序列的功率譜: 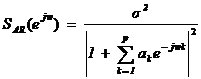 , ,
式中,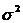 為白噪聲序列方差。AR模型估計中,由于隱含自相關函數的外推,而使分辨率大大提高;從而觀測數據的多少對分辨率影響不大,但對估計誤差會有影響,數據越多,估計誤差越小。AR模型中階數p越低,功率譜分辨率降低,但譜的平滑性變好,估計誤差降低。 為白噪聲序列方差。AR模型估計中,由于隱含自相關函數的外推,而使分辨率大大提高;從而觀測數據的多少對分辨率影響不大,但對估計誤差會有影響,數據越多,估計誤差越小。AR模型中階數p越低,功率譜分辨率降低,但譜的平滑性變好,估計誤差降低。 4、ARMA模型法 ARMA模型是既有零點,又有極點的模型。ARMA(p,q)的差分方程如下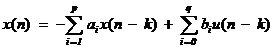 ,其中u(n-k)是零均值,方差為 ,其中u(n-k)是零均值,方差為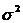 的白噪聲,p,q分別為自回歸(AR)和滑動平均(MA)的階數。由AR模型得到 的白噪聲,p,q分別為自回歸(AR)和滑動平均(MA)的階數。由AR模型得到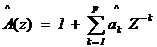 ,對已知數據uN(n),經過 ,對已知數據uN(n),經過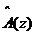 ,輸出y(n)近似于一個MA(q)過程,求出 ,輸出y(n)近似于一個MA(q)過程,求出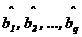 和輸入噪聲方差的估計 和輸入噪聲方差的估計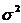 ,從而實現ARMA(p,q)模型的參數估計。得到 ,從而實現ARMA(p,q)模型的參數估計。得到 5、最大似然法(ML法) 最大似然法頻率估計是通過求解似然函數的最大值來進行頻率估計,此法對信噪比門限要求較低,不需要事先對噪聲進行學習,應用簡便,是最準確的頻率估計方法;但在求解最大似然函數最大值時要求解一個高度非線性化的方程,計算量非常大,有時甚至無法求解,不適用于實時計算。 設信號表示為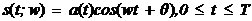 ,其中,a(t)已知;相位是在 ,其中,a(t)已知;相位是在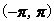 上均勻分布的隨機變量;頻率w是待估計的信號參量。接收信號表示為 上均勻分布的隨機變量;頻率w是待估計的信號參量。接收信號表示為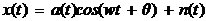 ,其中,n(t)是均值為零的高斯白噪聲。當頻率w為待估計量時,有 ,其中,n(t)是均值為零的高斯白噪聲。當頻率w為待估計量時,有 其中,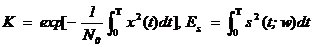 因為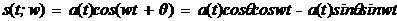 ,所以 ,所以 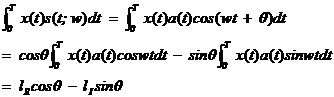 , ,由p[x(t)|w]對w求極大值就能得到頻率w的最大似然估計量。 6、多信號分類法(MUSIC算法) MUSIC算法利用信號子空間和噪聲子空間的正交性,構造空間譜函數,通過譜峰搜索,估計信號頻率。 根據觀測樣本值x(0),x(1),…,x(N-1),估計自相關矩陣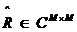 ;對 ;對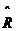 進行特征分解,得到(M-K)個最小特征值對應的特征向量,構造矩陣G;在 進行特征分解,得到(M-K)個最小特征值對應的特征向量,構造矩陣G;在 [-π,π]內改變w,計算SMUSIC(w),峰值位置就是信號頻率的估計值。 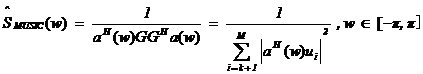
MUSIC算法是空間譜估計方法中極為重要的一種,分辨率高,對信號個數、噪聲干擾強度、相干關系等可以進行漸近無偏估計,在噪聲子空間大于信號子空間時,MUSIC算法有非常好的性能。但其需要在整個頻域內進行譜峰搜索,實時性較差。 7、旋轉不變子空間算法(ESPRIT算法) ESPRIT算法是基于旋轉不變技術的信號參數估計方法。首先,根據觀測樣本值x(0),x(1),…,x(N-1),估計相關矩陣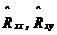 ;其次,對 ;其次,對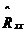 進行特征分解,計算得到最小特征值 進行特征分解,計算得到最小特征值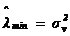 ;之后,構造矩陣對 ;之后,構造矩陣對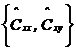 ,其中 ,其中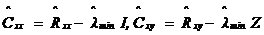 ;然后對 ;然后對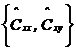 進行廣義特征分解,最接近單位圓的K個廣義特征值 進行廣義特征分解,最接近單位圓的K個廣義特征值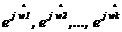 的相位給出了信號頻率的估 的相位給出了信號頻率的估 計。 ESPRIT算法具有較高的估計精度,無需像MUSIC算法一樣進行譜峰搜索,而是直接解出估計的信號頻率。但是ESPRIT算法需進行兩次特征值分解,計算量較大。 8、非平穩信號頻率估計方法 對于非平穩信號,不能簡單的使用平穩信號的估計方法,必須考慮時變因素。人們希望找到一個二維函數,既能反映信號的頻率內容,也能反映出該頻率內容隨時間變化的規律。其中最典型的是以Cohen類為代表的雙線性時頻分布,此分布可表示為 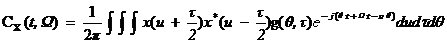
式中,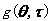 是一個二維窗函數,給定不同的窗函數可以得到不同的時頻分布。 是一個二維窗函數,給定不同的窗函數可以得到不同的時頻分布。 若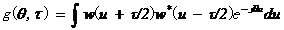 ,式中w是一個一維的窗函數,上式可以簡化為如下的譜圖 ,式中w是一個一維的窗函數,上式可以簡化為如下的譜圖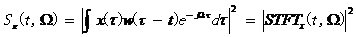 式中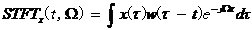 ,稱為信號x(t)的短時傅里葉變換,它 ,稱為信號x(t)的短時傅里葉變換,它 反映了信號的頻譜隨時間和頻率的分布。 短時傅里葉變換,它將分段加窗后的信號視為平穩信號,然后利用傅里葉變換進行分析,屬于線性變換,對地信噪比下的多分量信號有良好的分析能力,但是其時頻分辨率較低,存在窗口效應。 下面對MUSIC算法進行仿真說明,設被測量頻率為0.4Hz。 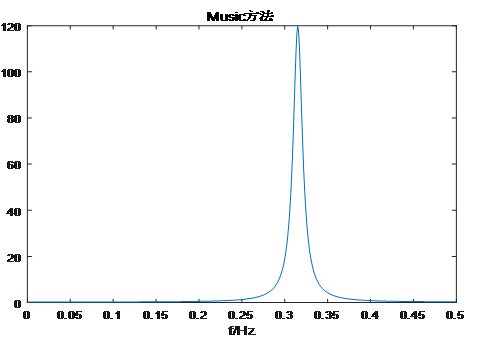
Snr=-20時,解出f=0.315Hz,實際f=0.400Hz,相對誤差15.25% 
Snr=-15時,解出f=0.412Hz,相對誤差7.5% 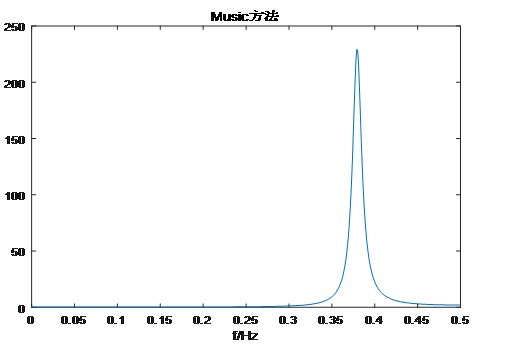
Snr=-10時,解出f=0.379Hz,相對誤差5.25% 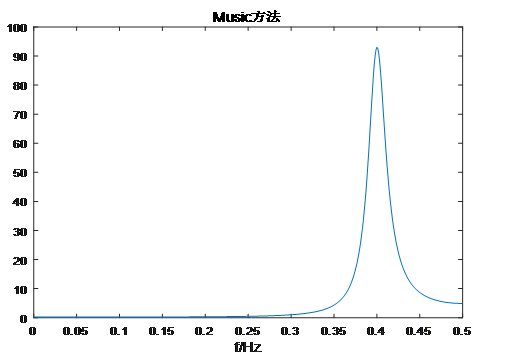
Snr=-5時,解出f=0.3920Hz,相對誤差2% 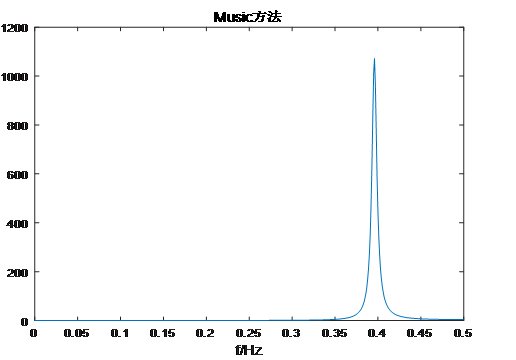
Snr=0時,解出f=0.3990Hz,相對誤差0.5% 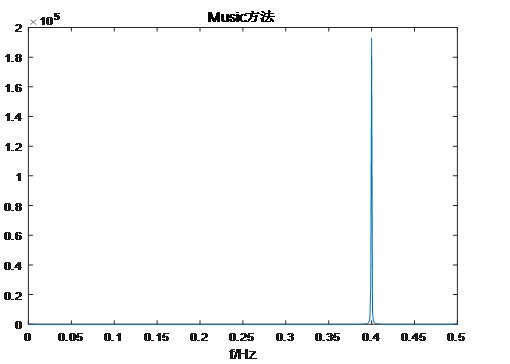
Snr=5時,解出f=0.400Hz,相對誤差0% 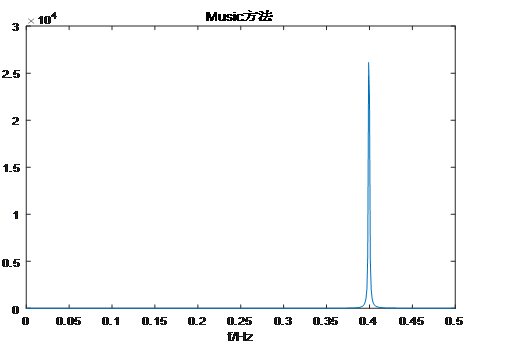
Snr=10時,解出f=0.400Hz,相對誤差0%。 在不同信噪比的情況下,計算1000組數據的相對誤差。 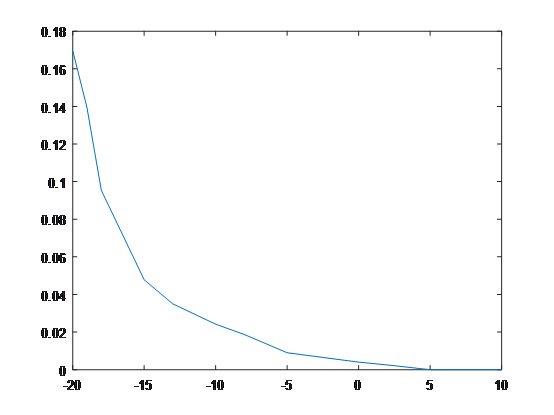
信噪比與相對誤差的關系,橫軸為信噪比,豎軸為相對誤差。
完整的Word格式文檔51黑下載地址:
 信號頻率估計.docx
(160.59 KB, 下載次數: 57)
信號頻率估計.docx
(160.59 KB, 下載次數: 57)
2018-8-7 09:32 上傳
點擊文件名下載附件
|