一、基本原理
CRC檢驗原理實際上就是在一個p位二進制數據序列之后附加一個r位二進制檢驗碼(序列),從而構成一個總長為n=p+r位的二進制序列;附加在數據序列之后的這個檢驗碼與數據序列的內容之間存在著某種特定的關系。如果因干擾等原因使數據序列中的某一位或某些位發生錯誤,這種特定關系就會被破壞。因此,通過檢查這一關系,就可以實現對數據正確性的檢驗。 二、幾個基本概念 1、幀檢驗序列FCS(Frame Check Sequence):為了進行差錯檢驗而添加的冗余碼。 2、多項式模2運行:實際上是按位異或(Exclusive OR)運算,即相同為0,相異為1,也就是不考慮進位、借位的二進制加減運算。如:10011011 + 11001010 = 01010001。 3、生成多項式(generator polynomial):當進行CRC檢驗時,發送方與接收方需要事先約定一個除數,即生成多項式,一般記作G(x)。生成多項式的最高位與最低位必須是1。常用的CRC碼的生成多項式有: CRC8=X8+X5+X4+1 CRC-CCITT=X16+X12+X5+1 CRC16=X16+X15+X5+1 CRC12=X12+X11+X3+X2+1 CRC32=X32+X26+X23+X22+X16+X12+X11+X10+X8+X7+X5+X4+X2+X1+1 每一個生成多項式都可以與一個代碼相對應,如CRC8對應代碼:100110001。 三、CRC檢驗碼的計算 設信息字段為K位,校驗字段為R位,則碼字長度為N(N=K+R)。設雙方事先約定了一個R次多項式g(x),則CRC碼: V(x)=A(x)g(x)=xRm(x)+r(x) 其中: m(x)為K次信息多項式, r(x)為R-1次校驗多項式。 這里r(x)對應的代碼即為冗余碼,加在原信息字段后即形成CRC碼。 r(x)的計算方法為:在K位信息字段的后面添加R個0,再除以g(x)對應的代碼序列,得到的余數即為r(x)對應的代碼(應為R-1位;若不足,而在高位補0)。 計算示例 設需要發送的信息為M = 1010001101,產生多項式對應的代碼為P = 110101,R=5。在M后加5個0,然后對P做模2除法運算,得余數r(x)對應的代碼:01110。故實際需要發送的數據是101000110101110。 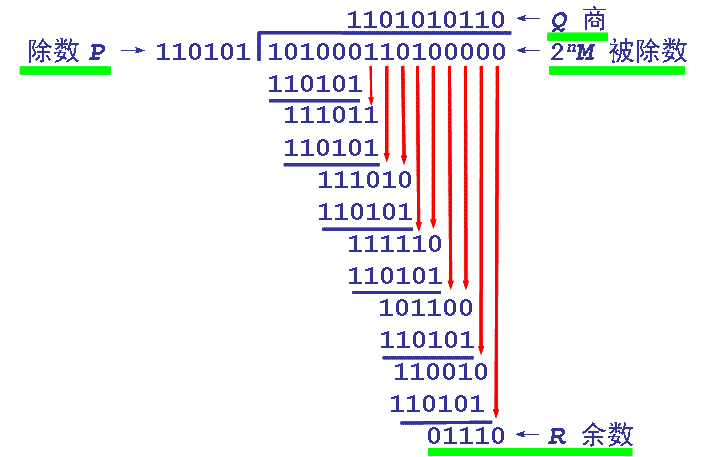
四、錯誤檢測 當接收方收到數據后,用收到的數據對P(事先約定的)進行模2除法,若余數為0,則認為數據傳輸無差錯;若余數不為0,則認為數據傳輸出現了錯誤,由于不知道錯誤發生在什么地方,因而不能進行自動糾正,一般的做法是丟棄接收的數據。 五、幾點說明: 1、CRC是一種常用的檢錯碼,并不能用于自動糾錯。 2、只要經過嚴格的挑選,并使用位數足夠多的除數 P,那么出現檢測不到的差錯的概率就很小很小。 3、僅用循環冗余檢驗 CRC 差錯檢測技術只能做到無差錯接受(只是非常近似的認為是無差錯的),并不能保證可靠傳輸。
線性編碼理論。在發送端傳送的K位二進制數據,以一定規則產生一個校驗監督碼(或者叫監督矩陣)r位,并負載信息后,構成一個新的二進制碼序列共(K+R)位。最后發送出去。在接收端根據信息嗎和CRC碼禁言,是否出錯。 CRC16監督式(美國標準):G(X)=X^16+X^15+X2+1 CRC16監督式(歐洲標準):G(X)=X16+X12+X5+1 一般多數采用CCITT推薦的歐標格式:10001000000100001 16位的CRC碼產生的規則是先把要發送的信息元左移16位(乘以2^16),再除以監督式,最后得到的是CRC碼。再把CRC碼附在信息元后面,一起發送出去。 B(X).2^16/G(X)=Q(X)+R(X)/G(X) Q(X)是商,R(X)是余數。模2加減法就是不帶進位借位的加減法相當異或,乘除法和普通數學乘除法一致。例如: 信息碼:1011,監督元:G(X)X^8+X^5+X^4+1 CRC8校驗 下面是除法運算: 1011 0000 0000 1001 1000 1 10 1000 1000 10 0110 001 11101010 所以CRC 8 監督元:11101010 發送的K+r位碼:1011 11101010 接收端接收到的信息碼除以監督元,如果R(X)為0,說明傳輸無誤。 假設接收到跟發送一致。驗證 1011 1110 1010 1001 1000 1 10 0110 0010 10 0110 001 0 所以接收正確無誤 實際通信中發送數據是多字節,比如發送地址、控制、信息、校驗。所以必須按多字節去計算CRC碼。
|