0.9,9循環,也就是0.999999999999999999……,這個無限循環小數我們見的不多,因為我們在直覺上都認為他會等于1。但是我們需要一些理由,千萬不要用"0.33333……=1/3,那么3/3=0.99999……=1"這種方法哦,因為這個說法似乎缺乏說服力。。。
我找出了以下幾種可行的方法:
(很久以前(大概小學三年級那會)我一直在思索這個問題,但學了微積分之后發現我能解決了。。)
1.無窮級數法

很明顯,這個級數收斂。

∞ 1
=9Σ ------
x=1 x
10
x
∞ 1
=9Σ ------
x=1 10
這樣就化成了幾何級數。
1
=9×----------- - 9
1
1 - -----
10
10
=9×---- - 9
9
=1
2.極限法(原理基本相同)
(注:這個圖中貌似有錯誤,應該把i前面的負號去掉。)
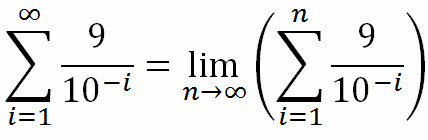 =1 =1
3.代數……(這是我見過的最簡潔,最簡單的證法………)
設x = 0.999……
10x = 9.999……
10x-x = 9.999……-0.999……
10x-x = 9
于是—— x=1 了……
如果你有一些奇妙的證法(想法),或者是有一些有趣的問題,可以說出來與大家分享。
|