RS編解碼的MATLAB實現與分析帶實驗報告與源碼

ID:140725 · 發表于 2016-10-11 18:16

所有資料下載（含實驗報告和仿真及源碼）：

RS編解碼的MATLAB實現與分析.rar (315.72 KB, 下載次數: 79)

《信息論與編碼》課程設計

RS編解碼的MATLAB實現與分析

中文摘要

RS碼全稱為Reed-Solomon碼，是由Irving Reed和Gus Solomon在1960年發明的。RS碼是差錯控制領域中一類重要的線性分組碼，具有較強的糾正突發錯誤和隨機錯誤的能力。特別是在短碼和中等長度碼的情況下，其性能接近于理論值。

由于RS碼采用了q進制（q=2m），所以它是多進制調制時的自然和方便的編碼手段。因為RS碼能夠糾正小于或等于t個的隨機差錯，或者糾正單個長度為（t-1）m+1的突發錯誤，所以適合于在衰落信道中使用，以克服突發性差錯。而且該碼具有各種成熟，可用，有效的譯碼算法。因此RS碼在工程中被廣泛應用，包括各種通信和計算機存儲系統中。特別是RS碼和卷積碼構成的級聯碼，已經被定義為深空通信的下行鏈路中的標準[1]。另外，歐洲數字視頻廣播DVB（-S/T/C）統一采用（204，188）RS碼。

本文將對RS碼的編解碼原理進行闡述，并運用MATLAB對RS碼進行仿真和分析。

Abstract

RS codes as Reed-Solomon code, found by Irving Reed and Gus Solomon in 1960. RS code is an important class of linear block codes in the field of error control code, with a strong capacity of correcting burst errors and random errors. Especially in the case of short and medium length code, the performance is close to the theoretical value.

Using a base-Q, RS codes are the natural and convenient means in a multi-ary modulation. RS code can correct a less than or equal to t random errors, or to correct a single length (t-1) m+1 burst error, so it is suitable for the use in the fading channel in order to overcome the unexpected errors. And that the codes have a variety of mature, available, efficient decoding algorithms. Therefore, RS codes are widely used in engineering, including various communications and computer storage systems. especially in concatenated codes which consists of RS code and convolutional code, has been defined as deep-space communications standards in the downlink[1]. In addition, the European Digital Video Broadcasting DVB (-S/T/C) uniform application of (204,188) RS codes.

This RS code and decoding will be explained the principle and the use of MATLAB code for simulation and analysis of RS is also includes in this principle

Key words: RS code,Correction,MATLAB

1. RS碼的發展和現狀[2]

根據香農提出的信道編碼定理，任意離散輸入無記憶平穩信道存在信道容量C，它標志著信道傳輸能力的上限，只要信息傳輸速率R<c，就存在一種編碼方式，當平均碼長足夠大時，譯碼錯誤概率可以做到任意��；反之，則無論采用何種編碼方式也不可能保證錯誤概率任意小。該定理雖然沒有明確指出如何對數據信息進行糾錯編碼，也沒有給出這種具有糾錯能力通信系統的具體實現方法．但它奠定了信道編碼的理論基礎，從理論上指出了信道編碼的努力方向。[ color][="" align]正由于目前其成熟的理論和技術，rs碼在現代數字通信、數據存儲系統中得到了廣泛的應用，具體應用[6]見表1.1。[="" 0)]表1.1[="" align]

應用領域	編碼方案
硬盤驅動器	RS(32，28)碼
CD	交叉交織RS碼(CtRC)
DVD	RS(208，192)碼，RS(182，172)碼乘積碼
DAB、DVB	內碼為卷積碼，外碼為RS(204，188)碼的級聯碼
ATSC	內碼為卷積碼，外碼為RS(207，187)碼的級聯碼
深空通信	內碼為卷積碼，外碼為RS(255，223)碼的級聯碼
光纖通信	RS(255，239)碼

3.研究RS碼的意義與目的[7]

在實際的通訊信道中，信號的傳輸會受到噪聲的干擾，從而在接收端不可避免地會發生錯誤。要使信號能可靠的傳輸，即要降低信號傳輸中的誤碼率。人們采用了一系列相關技術來改善噪聲信道的接收性能，使接收信息的誤碼率盡可能降低。這些技術中，信道的糾錯編碼及其譯碼方法處于非常重要的地位。自從1948年香農發表了關于信道容量理論極限的重要論文之后，短短幾十年時間里，人們在信道編碼研究領域相繼取得了眾多理論成果和突破。

信道編碼按照對信息元的處理方式不同，可分為線性分組碼和卷積碼，線性分組碼可以完全用代數方法來嚴格地表達，它的出現較早而且其譯碼方法也較為簡單，因此容易被人們所認識，現在有關線性分組碼的理論已經相當成熟。卷積碼雖然也早已出現，但由于其編碼結構不能較好的用代數方法表示，因此給卷積碼的理論研究帶來了一定的困難。但是，單獨的線性分組碼或卷積碼在性能上離香農理論極限還相差較遠。為了進一步提高編碼的糾錯性能，人們采用了不同的措施，其中將兩個編碼進行串行級聯是一種有效的方法。級聯碼一般采用Rs碼作為外碼，卷積碼作為內碼，因此可以同時糾正隨機和突發的混合錯誤。但是這種形式的級聯碼，對改善單個碼元的誤碼率仍沒有太大幫助。如何對現有的編碼方法進行改進，從而更加逼近香農理論極限，已經成為國際通信學界的重大課題。

RS碼具有很強的抗突發誤碼的能力，因此被廣泛應用于各種通信領域。正因為RS編碼的應用范圍非常廣泛，對于RS編／解碼技術的研究一直是國內外通信系統研究的一個熱點，特別是RS編／解碼的硬件設計更是其中之重點和難點。

4.基礎理論4.1 RS編碼

RS編碼是一種線性的塊編碼[8]，其表示形式為RS(n，k)。當編碼器接收到一個數據信息序列，該數據信息序列被分割成若干長度為k的信息塊，并通過運算將每個數據信息塊編碼成長度為k的編碼數據塊。在RS碼中的碼元符號不是二進制而是多進制符號，其中2m進制使用更為廣泛。RS碼是建立在GF(2m)上(m>=3，m是任意整數)有限域上，且RS碼是MDS碼，具有極大最小距離特性，它具有卓越的糾錯能力，無論是糾突發錯誤還是糾隨機錯誤的能力，以及它的快速譯碼速度，均是其它碼類無法比擬的。用MS多項式產生的是非系統碼，而用BCH構造方法能產生系統碼。我們用的是后一種。

RS碼的定義：GF(q)上的(q≠2，q=2m)，碼長n=q-1的本原BCH碼成為RS碼[2]。可知RS碼最主要的特點之一是碼元取自GF(2m)上，而它的生成多項式也在GF(q)上，所以RS碼是碼元的符號域與根域一致的BCH碼。

因為

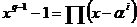
，（其中

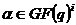
）的最小多項式

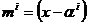
。所以，碼長為N=q-l，校驗位n-k=2t，設計距離為

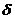
的RS碼，最小距離dmin=n-k+1。由BCH碼的定義可知，它的生成多項式為

從RS碼的n、k值立即可斷定其糾錯能力為

t=int[(dmin-1)/2]=int[(n-k)/2]

由此生成一個q進制的[q-1，q-]RS碼，有最小距離。由于線性碼的最大可能的最小距離是校驗元的個數加l，而RS碼恰好做到了這一點。因此，稱RS碼為極大最小距離可分碼，簡稱MDS碼。顯然RS碼的設計距離與實際距離D是一致的。如果我們要設計一個=9的RS碼，顯然RS碼的冗余位為-1=8=2t它的生成多項式為：

將信息段看成信息碼多項式m(x)，即

用信息碼多項式m(x)除以生成多項式g(x)，所得余式r(x)為監督碼多項式，即

將監督碼多項式r(x)置于信息碼多項式之后，形成RS碼。

4.2 RS譯碼

RS解碼可分為時域解碼和頻域解碼。時域解碼直接根據接收到的數據確定錯誤位置，不需要轉換計算，相對較容易實現。反之，頻域解碼首先要確定錯誤位置的傅氏變換，然后通過傅氏反變換找到錯誤位置，因此一般采用時域解碼[9]。

本文RS碼譯碼算法采用Berlekamp算法[10-11]，該算法是從計算接收碼字得到的伴隨式入手，以下我們用c(x)表示碼字，e(x)表示有

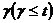
個錯誤得錯誤圖樣，r(x)表示接受字，r(x)=c(x)+e(x)，

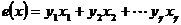
其中xi是第i個差錯得錯誤位置，定義

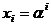
，yi是它的錯誤值。

（1）根據接收到的碼多項式計算伴隨式S

而計算伴隨式之值{Sp}(p=1,2,…，2t-1,2t),就是將碼得規定根代入多項式r(x) ，則得，

若S=0，認為接收無誤。若

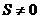
，則由S找出錯誤圖樣。

因為

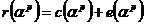
，而

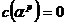
（p=1,2,…，2t）

即

從本質上說，譯碼器就是求解伽邏華域GF（2m）上得這組伴隨式非線性聯立方程，由伴隨式S找出錯誤圖樣時，先確定錯誤位置。

由于RS碼是由伽邏華域GF（2m）上某個元素的2t個連續冪次為根的生成多項式所定義的，用這些根取估算一個碼字多項式時，可寫出xi再求錯誤值yi。一般避免直接求解錯誤位置xi，而代之以間接法。

（2）從伴隨式S到差錯位置多項式

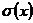
的迭代算法

錯誤位置多項式為：

顯然，差錯位置多項式的v個根式差錯位置數的倒數

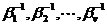
。各次項的系數

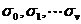
和

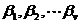
一樣是未知數。將②式展開可得：

再將③式代入①式可得牛頓恒等式：

令第μ次迭代后所得

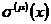
是

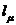
次多項式為

這時，

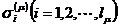
表示第μ次迭代后所得得i次項系數。得系數一定滿足式③得前μ個牛頓恒等式，但不一定滿足第μ+1個牛頓恒等式。為了求

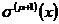
，先求第μ次迭代的差值

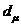
如下：

差值實際上就是將第μ次迭代的結果代入最后一個牛頓恒等式所得的結果。

如果=0，說明的系數也滿足第μ+1個牛頓恒等式，校驗通過。這時可令

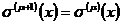
，如果

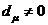
，說明的系數不滿足第μ+1個牛頓恒等式，差距是，這時要求做修正并求修正后的。修正后的取法是：

I．從本次的迭代回退，尋找前面某一次，比如第ρ次迭代（ρ<μ）的差錯多項式

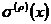
，要求該次（即第ρ次）迭代差值且

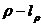
最大。

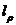
是第ρ次迭代時多項式

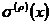
最高項的次數，即

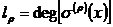
II．取修正項為

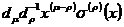
，即令：

式中，

，

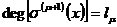
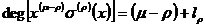
，的最高次為：

（3）利用錯誤位置多項式求出差錯位置數

將得到的錯誤位置多項式的系數代入式①，可算得

（4）利用伴隨式和

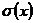
的系數求出差錯幅值

由式④和式⑤，可得：

比較它們得同次項系數，再代入①式，即可得：

根據⑥式即可求得差錯幅值。

5.模塊組合

本文采用RS（7，3）碼進行仿真，各模塊組合及其仿真流程圖如圖1所示：

圖1

其中，RS編碼與解碼已經在基礎理論中做了介紹，下面著重對其他組合模塊的功能和產生進行簡單的介紹。

5.1 多進制信源

用MATLAB自帶函數rand產生隨機數，乘以M（所要產生的進制數），再經過向下取整即可。

5.2 將多進制信息進行分幀

由于多進制信源產生的是一連串的多進制符號，為了進行編碼，需將這些符號進行分組，本次設計采用MATLAB自帶函數reshape, 將信息串（本次設計采用12000）變換成一個矩陣，該矩陣的行數為幀數（本次設計取值為4000），列數為信息位數（本次設計取值為3）

5.3 PSK傳輸系統

圖2

（1）8PSK調制器

I.首先將RS編碼器的輸出，映射到數域。然后把每個八進制符號都映射成三個二進制符號，映射規則如表2所示：

八進制符號	二進制符號
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

表2

II.再將每三個二進制符號按圖三進行映射。

（2）高斯隨機數發生器

同時產生高斯隨機數的同相分量和正交分量。

（3）為了驗證RS碼在突發差錯情況下仍然保持良好性能，故在PSK傳輸系統中引入突發差錯，與未加突發差錯的情況形成對比。

（4）判決器

計算接受信號在發送向量的投影，判斷哪個投影最大，就判哪個向量輸出。

圖3

5.4 將信息幀合并一串信息

由于從RS譯碼器輸出的消息是分組的，應將這些消息進行合并，以便與信源產生的消息進行比較，計算誤碼率。

5.5 誤碼率計算

只要將上述輸出與信源比較，計算有多少不同的符號，然后再除于信源產生的符號數，即得誤碼率。

6.結果分析

根據以上仿真過程，采用信源產生N=

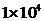
（為節約程序運行時間，故N取值較�。﹤€符號，固定信號功率S=1，得出以下圖表。

經RS編碼后，信道采用pskmoto.m文件，信息流通過未加隨機差錯的曲線如下圖所示：

圖4

經RS編碼后，信道采用pskmoto2.m文件，信息流通過加上隨機差錯的曲線如下圖所示：

圖5

對比兩圖可見，未加突發差錯和加上突發差錯的信噪比與誤碼率曲線圖相差不多，故得出結論，RS編碼對突發差錯具有良好的抵抗能力。

7.總結

通過本次課程設計的學習讓我了解了RS編碼的歷史、原理和編碼的步驟還有它的實際應用和不足之處、也使我對RS編碼有了重新的認識。通過本課程的學習，我也認識了自己還有很多不足，需要進一步學習的地方，在接下來的學習中我會花更多時間，我要不斷的努力，多聯系，多思考，來認真加深知識理解與運用，我相信我能有所進步的。

參考文獻

[1] 蘇艷琴等．基于RS碼和LDPC碼的糾錯性能分析．海軍航空工程學院電子信息工程系．

[2] 陳曦．基于RS編碼的光通信系統的設計與實現：[碩士學位論文]．成都：電子科技大學，2009

[3] Xu Youzhi．Implementation of Berlekamp-Massey algorithm without inversion．1EE E

Proceedings-I，1991，138(2)：138-140

[4] Hsie-Chia Chang，C．Bernard Shung．New Serial Architecture for the Berlekamp-Massey

Algorithm．IEEE Transactions on communications，1999，47(4)：48 1-483

[5] DiHp V Sarwate，Narcsh R Shanbhag．High-Speed Architectures for Reed-Solomon Decoders．

IEEE Transactions Very Large Scaleintegration(VLSD Systems，2001，9(5)：641-655

[6]陳飛，周德新．高速光網絡系統中FEC編碼器的設計與實現．光通信技術，2004，4(5)：35．37

[7] 曹立朋．數字視頻廣播傳輸系統中的的信道編碼技術：[碩士學位論文]．西安：西安電子科技大學，2006

[8] 曹雪虹，張宗橙．信息論與編碼．清華大學出版社．2004．

[9] 堯勇仕．DVB系統的RS編解碼的設計及ASIC實現：[碩士學位論文]．江蘇：江南大學，2008

[10] Marconetti, R. Guenard, D. Savage, P. Crowe, I. Epelde, L. Bradley, F. Cali.A fully programmable Reed Solomon 8-bit codec based on a re-shapedBerlekamp Massey algorithm. Proceedings of the IEEE InternationalSymposium on Circuits and Systems (ISCAS ’02), 2002, 5: 553-556.

[11] 朱起悅．RS碼編碼和譯碼算法．中國期刊網．1999．4．