完整的pdf格式文檔51黑下載地址（共7頁）：
卡爾曼濾波最詳細易懂的理解.pdf
(856.69 KB, 下載次數: 402)
2017-8-19 22:32 上傳
點擊文件名下載附件
下載積分: 黑幣 -5
下面是部分內容預覽（個人覺得寫得很好，很有用）：
不好意思，由于工作繁忙和文章不好組織的原因，拖了 2 個星期才更新。這一章要系統地去解釋卡爾 曼濾波，這個解釋應該是網上所有文章里面寫得最兼顧詳細和易懂的，但是卡爾曼濾波還是一個比較系統 的工程，需要讀者具備一定的耐心。
卡爾曼濾波有五個最基本的公式，我們將對其一一解讀。
0.png (16.79 KB, 下載次數: 174)
下載附件
2017-8-20 03:17 上傳
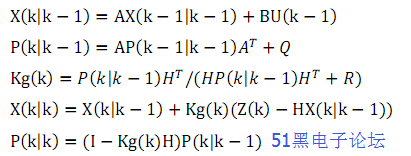
以上的公式看著很嚇人，但我將會對其進行通俗講解，看完會有滿滿收獲，所以請別跑開。
沒讀過本公眾號前兩篇文章的讀者最好先讀一下，可以方便理解這一篇文章，公眾號名稱是“電子搬 磚師”，可以用微信關注閱讀。本公眾號前兩篇文章都只是講如何用卡爾曼濾波對單種數據進行濾波處理， 然而工程上往往有多種數據需要同時濾波處理，比如加速度傳感器可以測量 3 個維度的加速度信息，這就 有 3 種信號需要做濾波處理。假設我們要對 n 種數據做卡爾曼濾波，我們應該怎么做呢？
我們可以用單種信號的卡爾曼濾波方程，連續寫 n 次，然后求取每種信號各自的濾波值。但是這么多
個方程寫出來會很龐大，因此我們就用矩陣的方式來描述，矩陣可以將 n 個方程組整合成一個方程，如下圖所示：
0.png (101.74 KB, 下載次數: 143)
下載附件
2017-8-20 02:56 上傳
0.png (86.95 KB, 下載次數: 146)
下載附件
2017-8-20 02:56 上傳
圖中 n 個方程組最終化簡成一個矩陣表達式：AX=B，矩陣表示是不是很簡潔？卡爾曼濾波的五個基本 公式中的 X,A,B,U,P,Q,Kg,H,R,Z,I 就都是矩陣，即五個公式其實是五個方程組。
這里還需要知道一個概念叫向量，向量是一維的矩陣，如下圖所示：
0.png (167.83 KB, 下載次數: 136)
下載附件
2017-8-20 02:57 上傳
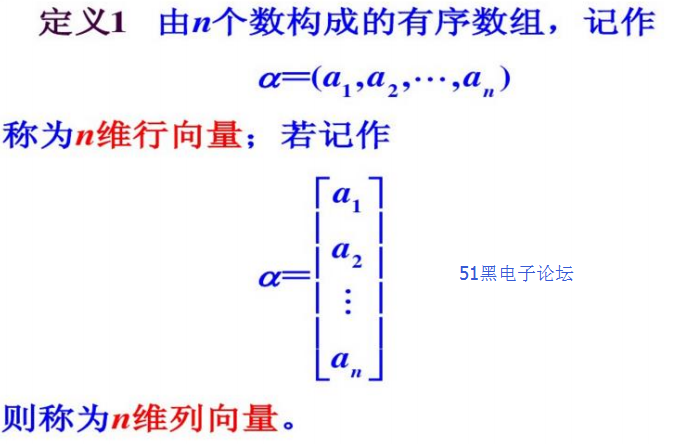
卡爾曼濾波的五個公式中的 X,U,Z 都是一維矩陣，也就是向量。 最后還需要知道一個概念叫做矩陣轉置，如下圖所示：
0.png (94.12 KB, 下載次數: 147)
下載附件
2017-8-20 02:57 上傳
至此我們擁有了可以理解卡爾曼濾波最基礎的條件了，我們正式進入正題。 我們開始理解第一個公式：X(k|k − 1) = AX(k − 1|k − 1) + BU(k − 1)。 假設你要對飛機的歐拉角進行卡爾曼濾波，你可以用傳感器先獲取到一個歐拉角和角速度的初始值，
并把這個值當做上一時刻(k-1)的值，然后根據上一時刻(k-1)的值你可以估計出這一時刻(k)飛機的歐拉角為：
Pitch(k)=Pitch(k-1)+GyroY(k-1)*dt Roll(k)=Roll(k-1)+GyroX(k-1)*dt Yaw(k)=Yaw(k-1)+GyroZ(k-1)*dt
Pitch 是俯仰角，GyroY 是俯仰角對應的角速度，dt 是 k-1 到 k 的時間
Roll 是滾轉角，GyroX 是滾轉角對應的角速度，dt 是 k-1 到 k 的時間 Yaw 是偏航角，GyroZ 是偏航角對應的角速度，dt 是 k-1 到 k 的時間 我們想辦法將上面的方程組簡化成矩陣表示：
設(k|k-1)代表這一時刻根據上一時刻的估計值，(k-1|k-1)代表上一時刻卡爾曼處理得到的最優值（這 里由于才開始第一輪的濾波準備，沒有上一時刻卡爾曼處理得到的最優值，就將 k-1 時刻測量到的值直接 當做最優值），(k-1)是上一時刻實測值，令：
0.png (25.97 KB, 下載次數: 152)
下載附件
2017-8-20 02:58 上傳
則上面三個方程組就可以表示為X(k|k − 1) = AX(k − 1|k − 1) + BU(k − 1)，請注意這里 A 與 B 不一
定要是對角線才有值的矩陣，只是在這個簡單例子中是這樣的。 其中：
X(k|k − 1)就是指根據上一時刻估計出這一時刻的估計值向量。
A 是上一時刻狀態轉移到這一時刻狀態的狀態轉移矩陣。
X(k − 1|k − 1)是上一時刻的最優值向量，如果卡爾曼濾波是第一次執行，就不存在上一時刻處理得到 的最優值，只能推薦將傳感器上次獲取到的值當做最優值。
B 是控制量矩陣。
U(k − 1)是上一時刻控制量測量值向量。 至此，第一個公式已經理解。
我們開始理解第二個公式：
0.png (2.32 KB, 下載次數: 144)
下載附件
2017-8-20 02:59 上傳
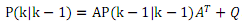
回到 n 種數據做卡爾曼濾波的主題。依據 k-1 時刻的值我們可以得到 k 時刻的估計值，但是這個估計 值和真實世界的值含有兩種誤差，一種誤差是 k-1 時刻真實世界值 X(k-1)和最優值 X(K-1|K-1)之間的誤差， 還有一種誤差是控制量及其對時間積分造成的誤差，后者誤差我們用誤差向量 W(k-1)表示：
0.png (3.35 KB, 下載次數: 133)
下載附件
2017-8-20 03:00 上傳
0.png (166.32 KB, 下載次數: 166)
下載附件
2017-8-20 03:02 上傳
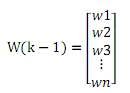
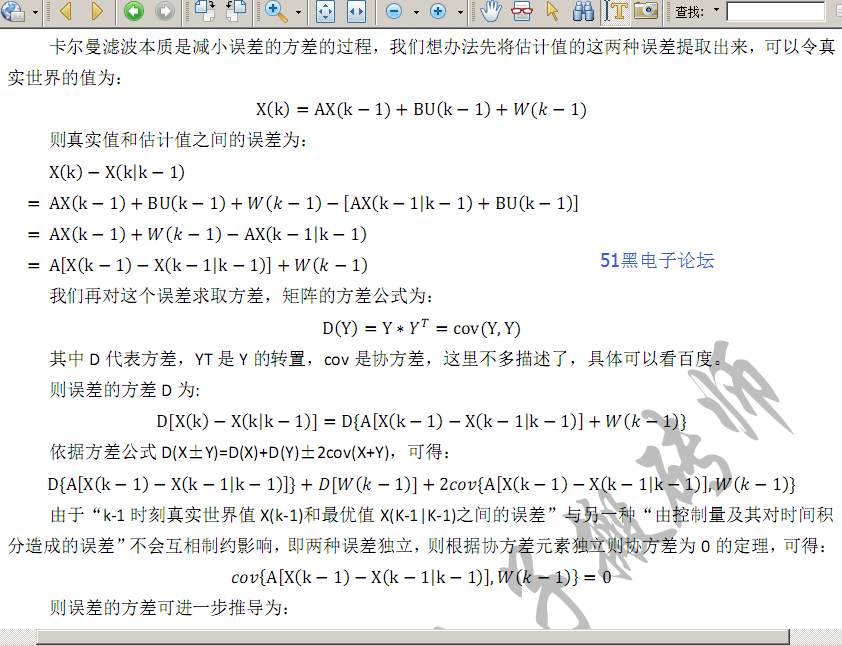
至此，第二個公式已經理解。 這回特殊，我們要先理解第四個公式，后面會再回頭理解第三個公式，原因后面看著看著就能明白了。
第四個公式是：X(k|k) = X(k|k − 1) + Kg(k)(Z(k) − HX(k|k − 1))
在理解第四個公式前，需要拿傳感器先測量下這一時刻的值，設這一時刻傳感器的測量數據向量為 Z(k)。 由于有些時候 X(k)向量中有一些元素是沒法用傳感器直接測量得到的，但是這個元素又可以利用傳感器的 其它測量值推算出來，因而我們將這一時刻傳感器的測量數據向量定義為：
Z(k) = HX(k) + V(k)
其中 H 就可以修飾 X(k)中某些元素不能通過傳感器直接測量得到，通常 H 矩陣的斜對角元素是由 0 和
1 構成的，0 就代表對應元素無法用傳感器直接測量，1 代表對應元素可以用傳感器直接測量。V(k)向量代 表傳感器測量誤差，比如稱重秤的誤差為 10g，這 10g 就是這個 V(k)。
那這第四個公式在邏輯上就很好理解。先用這一時刻傳感器的測量值減去根據上一時刻估計出來的值， 得到殘差，然后用一個比例系數矩陣 Kg 乘上這個殘差，再加上根據上一時刻的估計值，就可以得到這一時刻最有可能的值，也就是最優值。這個最優值既不完全相信傳感器，也不完全相信估計值，只要控制好比
例系數，就能得到最適合的值。 至此，第四個公式已經理解。 我們開始理解第五個公式：P(k|k) = (I − Kg(k)H)P(k|k − 1)。
回顧下之前第二個公式中的 P(k|k-1)，是代表上一時刻的估計值和此刻真實世界值的誤差的方差。而
P(k|k)代表此刻計算得到的最優值和此刻真實世界值的誤差的方差。
0.png (129.13 KB, 下載次數: 156)
下載附件
2017-8-20 03:03 上傳
由于卡爾曼濾波是一個不斷減小最優值和此刻真實世界值的誤差的方差的過程，P(k|k)是最優值和此 刻真實世界值的誤差的方差矩陣，其對角線元素就是各個元素各自的誤差的方差。為了讓所有元素的方差 最小，我們把每個元素的方差都加起來，即把 P(k|k-1)的對角元素方差加起來，求取總的方差值，只要方差 值總和最小，則就實現了最優值和此刻真實世界值的誤差的方差最小化的目的。將方差矩陣對角元素相加 的做法也稱為矩陣的跡，通常用 tr 表示。則:現在，這個由方差矩陣對角元素總和組成的tr,P(k|k)-函數需要取最小值，他的大小收到 Kg(k)這個權 重矩陣的影響，我們必須找到最適合的 Kg(k)使得和值最小。
數學上有導數為 0 取極值的方法，如下圖所示：
（請下載附件查看）
|
[復制鏈接]
QQ好友和群
QQ空間
騰訊微博
騰訊朋友
收藏
淘帖
頂
踩
